Forward Passes and Backpropagation in Neural Networks
Let $f$ be a function of $n$ inputs $x = (x_1, …, x_n)$. Then $f$ is the result of a sequence of binary operations and compositions on $x$.
To help visualize backpropagation, we can encode these binary operations and compositions in a graph, with the inputs on one end and $f(\cdot)$ on the other. Below is one example.
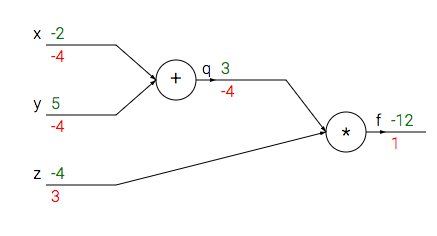
The minor complication is that, in general, some function like $g = x_1+x_2$ can be represented several times in $f$ (eg, $f = (x_1 + x_2)^2 + \frac{x_3}{x_1+x_2}$). Should we treat each instance of $g$ as the same node, or separate nodes? It depends on whether you want cycles in the graph. If our graph permitted cycles, we could have a single node for $g$ with multiple paths to $f$. Otherwise, we could have a separate node for each instance, and ultimately two sets of the input nodes $x_1$ and $x_2$.
I prefer to think about trees (I’ll explain why shortly), so let us exclude cycles, ie we consider every instance of a function as a different node. A tree $G=(V, E)$ can be constructed such that, for $x=t$, the values and partial derivatives of the inputs, intermediate values, and final output are easily computed and stored. So, a node $v$ associated with function $q$ stores:
- the output of $q| _ {x=t}$, computed via a simple operation on $v$’s children; and
- $\frac{\partial f}{\partial q}| _ {x=t}$, computed as the product of $\frac{\partial f}{\partial r}| _ {x=t}$ (stored in $\text{parent}(v)$) and $\frac{\partial r}{\partial q}| _ {x=t}$, where $r$ is the function associated with $\text{parent}(v)$.
The forward pass is simply computing (1) for all nodes (from $x$ to $f$). Backpropagation is computing (2) for all nodes (from $f$ to $x$). Backpropagation requires knowing the values of the intermediate functions at each node, so the forward pass must be done first.
There’s nothing in the tree so far that takes into account that different nodes can be representing the same function. For example, the tree representation of $f = (x_1 + x_2)^2 + \frac{x_3}{x_1+x_2}$ will be isomorphic to that of $h = (x_1 + x_2)^2 + \frac{x_3}{x_4 + x_5}$. The multivariable chain rule says that to find $\frac{\partial f}{\partial x_i}$, we need to add up the (2) values at every duplicate node of $x_i$ (which are generally different). If $x_i$ appears $n$ times in $f$, there will be $n$ duplicate nodes. (The same procedure applies to a partial derivative with respect to some intermediate variable (eg $g = x_1+x_2$.))
If we didn’t prefer trees, $G$ could contain cycles rather than duplicate nodes. Then the partial derivatives of some variable would be computed by summing the (2) values for each “parent” (now that a node can have more than one). I find it confusing to draw graphs with a bunch of cycles when I could mindlessly draw a tree and add up (2) values at nodes with the same label.